|
|
|
Visual
Cryptography
 Visual cryptography is a popular solution for image encryption. Using
secret sharing concepts, the encryption procedure encrypts a secret
image into the so-called shares which are noise-like secure images which
can be transmitted or distributed over an untrusted communication
channel. Using the properties of the human visual system to force the
recognition of a secret message from overlapping shares, the secret
image is decrypted without additional computations and any knowledge of
cryptography.
Visual cryptographic solutions operate on binary or binarized
inputs. Therefore, natural (continuous-tone) images must be first
converted into halftone images by using the density of the net dots
to simulate the original gray or color levels in the target binary
representation. Then, the halftone version of the input image is
used instead of the original secret image to produce the shares. The
decrypted image is obtained by stacking the shares together. Because
binary data can be displayed either as frosted or transparent when
printed on transparencies or viewed on the screen, overlapping
shares that contain seemingly random information can reveal the
secret image without additional computations or any knowledge of
cryptographic keys. However, due to the nature of the algorithm, the
decrypted image is darker, contains a number of visual impairments,
and most of visual cryptography solutions increase the spatial
resolution of the secret image. In addition, the requirement for
inputs of the binary or dithered nature only limits the
applicability of visual cryptography.
|
| |
 |
® |
 |
® |
 |
+ |
 |
= |
 |
|
| |
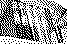Secret image |
|
Halftone |
|
Share 1 |
|
Share 2 |
|
Decrypted image |
|
Most of the existing secret sharing schemes are
generalized within the so-called {k,n}-threshold
framework that confidentially divides the content of a secret
message into n shares in the way that requires the presence
of at least k, for k≤n, shares for the secret
message reconstruction, Thus, the framework can use any of n!/(k!(n−k)!)
possible combinations of k shares to recover the secret
message, whereas the use of k−1 or less shares should not
reveal the secret message. |
| |
 |
® |
 |
® |
 |
+ |
 |
= |
 |
|
| |
Secret image |
|
Halftone |
|
Share 1 |
|
Share 2 |
|
Decrypted image |
|
|
|
References: |
|
 |
R. Lukac and K.N. Plataniotis, Secure Color Imaging. In Color
Image Processing: Methods and Applications, (eds.) R. Lukac and
K.N. Plataniotis, CRC Press / Taylor & Francis, pp. 185-202, October 2006. ISBN 0-8493-9774-X |
| R. Lukac, K.N. Plataniotis, and C.N. Yang,
Image Secret Sharing. In Encyclopedia of Multimedia, (ed.) B. Furth, Springer-Verlag,
pp. 328-335, January 2006. Including short articles:
Compression in Image Secret Sharing (pp. 86-87), Halftoning-Based Visual Secret
Sharing (pp. 363-364), Image Watermarking Using Visual Cryptography
(pp. 337-338), Private-Key Cryptosystem (pp. 712-714), Threshold
Schemes with Minimum Pixel Expansion (pp. 849-850), Visual
Cryptography (pp. 950-951). ISBN 0-387-24395-X |
| R. Lukac and K.N. Plataniotis, "Bit-Level Based Secret Sharing for Image Encryption," Pattern Recognition, vol. 38, no. 5, pp. 767-772, May 2005. |
| R. Lukac and K.N. Plataniotis, "Image Representation Based Secret Sharing," Communications of the CCISA
(Chinese Cryptology & Information Security Association), Special
Issue on Image Secret Sharing and Quantum Cryptography, vol. 11, no. 2, pp. 103-114, April 2005. |
|
|
|
